For this groundwater model the analytic element methodology is selected (Bakker, 2013) using the open-source implementation available in TTim (Bakker, 2015). The groundwater flow equations are solved based on the representation of internal boundary conditions, points, lines or polygons where constant groundwater level, constant flux or flux dependence on groundwater level is imposed. The resulting groundwater flow equations can be evaluated at arbitrary points in space and time. The solution is therefore independent of a spatial and temporal discretisation of the model domain and time into grid and time steps.
For finite-difference or finite-element groundwater models, the computational time is dominated by the number of grid cells and the number of time steps. The computational effort for the GW AEM is split between the time needed to solve the groundwater equations, which is related to the complexity of the representation of the internal boundaries, and the time needed to evaluate these equations at the required model nodes and times. In this case, a single evaluation of the transient analytic element model takes about 15 minutes.
Product Finalisation date
- 2.6.2.1 Methods
- 2.6.2.2 Review of existing models
- 2.6.2.2.1 Alpha and Kevin's Corner model review
- 2.6.2.2.2 Carmichael model review
- 2.6.2.2.3 China First model review
- 2.6.2.2.4 China Stone model review
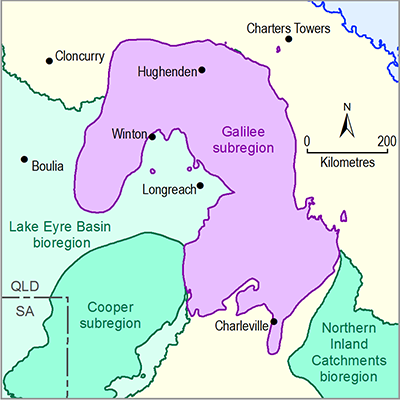
- 2.6.2.2.5 South Galilee model review
- 2.6.2.2.6 Galilee Basin hydrogeological model review
- 2.6.2.2.7 Suitability of existing groundwater models
- References
- Datasets
- 2.6.2.3 Model development
- 2.6.2.4 Boundary and initial conditions
- 2.6.2.5 Implementation of the coal resource development pathway
- 2.6.2.6 Parameterisation
- 2.6.2.7 Observations and predictions
- 2.6.2.8 Uncertainty analysis
- 2.6.2.9 Limitations and conclusions
- Citation
- Acknowledgements
- Currency of scientific results
- Contributors to the Technical Programme
- About this technical product
