3 Qualitative mathematical modelling (stage 2)

In this work we have been guided by a strategy of model building that recognises a practical trade-off between realism, generality and precision when building and analysing models of complex systems (Levins, 1966, 1998). To obtain a manageable and useful model, one typically sacrifices one attribute for the other two. Qualitative mathematical models emphasise generality and realism, but lack precision, while numerical simulation models can be both precise and realistic but are not generalisable (i.e. application of the model to changed circumstance requires reparameterisation). A third approach is statistical, and emphasises precision and generality. Here there are precise insights into the general pattern of correlations among variables, but at the cost of causal understanding of the processes involved. In practice we seek a robust strategy that considers combinations of different modelling approaches, such that models are mutually informative and build upon the strengths and insights of other approaches. The impact and risk analysis for BAs is being informed by all three modelling approaches. In this section we describe the basic methods underpinning qualitative mathematical modelling.

Qualitative mathematical modelling serves three roles within BA’s receptor impact modelling strategy. Firstly, sign-directed graphs (e.g. see Figure 5), built for each potentially impacted landscape class, document current understanding of how the landscape class ecosystem ‘works’ including key interactions between the system’s physical, chemical and biological components, and their dependence on hydrology.

Secondly, through qualitative predictions of increase, decrease or no change, the models capture the direct and indirect effects that are anticipated to occur following a sustained change to the surface water or groundwater regimes that maintain the ecosystem of the landscape class. Lastly, BAs use the hydrological factors identified in the models, and the direct and indirect effects that they predict, to identify appropriate hydrological response variables and receptor impact variables for the next stages of the receptor impact model strategy.

The BA methodology (Barrett et al., 2013) requires an explicit assessment of the potential direct, indirect and cumulative impacts of CSG and coal mining development on water resources, together with an analysis of the associated uncertainties. A coherent analysis of uncertainty necessitates a probabilistic analysis, so in effect the BA methodology requires a probabilistic landscape-level assessment of the risks that coal resource development poses to water resources. The BA methodology goes on to define direct impacts as those associated with CSG and coal mining developments that impact on natural resources without intervening agents or pathways, whilst indirect impacts are defined as those impacts on receptors (within water-dependent assets) that are produced as a result of a (simple or complex) pathway of cause and effect.

It is important to recognise that the BA methodology sets an ambitious target, seeking to predict how direct, indirect and cumulative impacts on hydrology by development affect receptors at multiple time points, but does not describe how to meet it. The receptor impact modelling strategy is designed to operationalise the aspirations of the BA methodology, and this process begins by distinguishing direct and indirect impacts in a conceptual model of the potential stress imposed on the ecosystem by coal resource development.

Qualitative mathematical modelling depicts the stressor conceptual model as a sign-directed graph wherein the direct effects between model variables are depicted as arcs ending in an arrowhead for positive direct effects, and arcs ending in a filled circle for negative direct effects (Section 3.1.1). The potential direct effect of coal resource development is identified by at least one negatively or positively signed arc between a hydrological response variable and one or more of the model’s other variables.

Within the sign-directed graph, a pathway with one arc is formally defined as a ‘direct effect’, whereas a pathway consisting of two or more arcs, which must therefore involve other intermediate variables, is formally defined as an ‘indirect effect’ (Section 3.1.1). The direct impacts of coal resource development are thereby depicted within the sign-directed graph as arcs of length one between a hydrological response variable and another model variable. Indirect impacts are identified as arcs of length two or more between a hydrological response variable and another model variable. Finally, cumulative impacts are depicted by changes to two or more potentially interacting hydrological response variables, with concomitant direct and indirect impacts arising from this.

When considering potential changes (perturbations) to the hydrological response variables that maintain landscape class ecosystems, it is important to distinguish between ‘press’ and ‘pulse’ perturbations. A press perturbation is defined as a sustained, or long-term, change in the value of a biological or physiochemical parameter that is associated with one or more variables that causes a shift in the equilibrium values of the system’s variables. This is in contrast to a pulse perturbation, which is a sudden increase or decrease in a variable that only moves the system away from its equilibrium temporarily, but does not necessarily result in a permanent shift to a new equilibrium state. Press-type perturbations are typically defined in terms of experimental manipulations of ecosystems (Dambacher et al., 2002; Schmitz, 1998). In a BA qualitative model, press perturbations are caused by CSG or coal mine induced changes to hydrological response variables. It is acknowledged that pulse perturbations and other categories of disturbance, such as ramp disturbance (Lake, 2000), are also of interest to BA. Press perturbations and other perturbation types may be assessed by the quantitative receptor impact model methodology described in the following chapters.

The distinction between press and pulse perturbations is important because the direct and indirect effects of pulse perturbations are typically minimal or short-lived. These perturbations typically occur over time frames that are much smaller than the generation time of the biological variables of interest. Unless the magnitude of the perturbation is so large that the system is moved to a new equilibrium state, there will be no permanent shift in the equilibrium level of the system variables, but only transient variations in their levels of abundance.

The Bioregional Assessment Programme, however, is principally concerned with press perturbations – that is, changes in hydrological response variables that are sustained for a relatively long time period, say many decades – and hence over much larger time frames than the generation times of the potentially impacted biological variables. The sustained nature of this type of perturbation provides time for the knock-on effects to be felt throughout the entire system. Although the quantitative receptor impact modelling strategy may account for both press and pulse perturbations (see following chapters), the implementation of the qualitative mathematical modelling focuses on press perturbations, and deliberately describes potential impacts on hydrological response variables in terms of changes in their long-term (e.g. 30 years) averages. Some pulse perturbations (e.g. the failure of a tailings dam) are assumed to be adequately managed by site-based risk management and mitigation procedures and are not assessed further in BAs.

This approach to defining and identifying direct, indirect and cumulative impacts is consistent with, and operationalises, the definitions in the BA methodology, and importantly provides a transparent platform for a coherent probabilistic analysis of direct effects (cumulative or otherwise) together with a qualitative mathematical analysis of indirect effects where relevant (see below).

3.1 Methods for qualitative mathematical modelling

The following section contains a brief overview of qualitative mathematical modelling based on the construction and analysis of sign-directed graphs (or signed digraphs) and also equivalent approaches using matrix algebra. The signed digraph models in this section are very simple models presented only for pedagogical purposes. Applied BA examples can be found in product 2.7 (receptor impact modelling) (Figure 3).

3.1.1 Signed digraph methods for qualitative mathematical modelling

3.1.1.1 System structure and signed digraphs

Qualitative mathematical modelling proceeds by first determining system structure, which is defined by the variables of the system and the relationships by which they are linked (Puccia and Levins, 1985). In biological systems, variables are typically interacting populations of different species, and their dynamics can be accounted for by generalised Lotka–Volterra equations, where each contributes towards the birth or death of another. Similarly, the dynamics of human social and economic systems can be described by the interactions of different sectors and entities of society that control flows of resources, goods and services.

The variables and relationships in a model system are portrayed by sign-directed graphs, or signed digraphs, where a link from one variable to another ending in an arrow () represents a positive direct effect, such as a rate of birth that is increased by consumption of prey, and a link ending in a filled circle () represents a negative direct effect, such as a rate of death due to predation. All possible ecological relationships can thus be described:

Self-effects are shown by links originating and ending in the same variable, and are typically negative, as in self-regulated variables, but can also be positive ( ), where variables are self-enhancing. Usually, relationships between species can be restricted to being linear (e.g. Lotka–Volterra predator–prey interactions), although non-linear relationships (e.g. Holling functional responses) can also be incorporated. Here, the sign of a relationship can change when the system passes a threshold. This then leads to construction and analysis of alternative model structures (Dambacher and Ramos-Jiliberto, 2007).

Once the structure of a system is defined, it is possible to analyse the system’s feedback which determines the qualitative conditions for system stability and perturbation response. These methods can proceed via analysis of the signed digraph through graphical algorithms or through equivalent algebraic analyses of the system’s community matrix. As an illustrative example, the Assessment team consider a signed digraph of a predator–prey community of size , where the top predator is an omnivore that feeds on the basal species (Figure 5):

Figure 5 A signed digraph of a predator–prey community of size n = 3, where the top predator N3 is an omnivore that feeds on the two other prey species

3.1.1.2 System stability

The stability of a system can be judged and understood according to criteria that depend on the relative sign and balance of the system’s feedback cycles (Puccia and Levins, 1985; Levins, 1974, 1975, 1998; Dambacher et al., 2003b). In general, stability requires that the net feedback in a system is negative and that feedback at lower levels is stronger than feedback at higher levels in the system. Negative feedback ensures that a system’s dynamics are self damped, and stronger feedback at lower levels ensures that a system will not over correct and exhibit unrestrained oscillations. The conditions can be interpreted through specific algebraic arguments. In general, though, stability in this system depends on the relative weakness of feedback cycles involving omnivory. Here, the feedback cycle has the potential to destabilise the system through positive feedback, and the feedback cycle , even though it is negative in sign, has the potential to introduce excessive higher level feedback if it is too strong.

3.1.1.3 Perturbation response

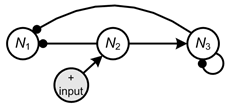
The signed digraph (or its matrix equivalent) provides a mechanism to predict qualitatively how species abundance or biomass in the system as a whole change as a result of a sustained change to the rate of birth, death or migration in any one of the species (Puccia and Levins, 1985; Levins, 1974, 1975, 1998; Dambacher et al., 2002). As an example perturbation scenario, consider a positive input to , such as food supplementation that increases its rate of birth. The qualitative effect of this input to the other variables is determined by accounting for all of the feedback cycles of length that emanate from . This is accomplished by tracing all paths from the input variable to a responding variable and multiplying each path by its complementary subsystem, the resulting product is defined as a feedback cycle. The complementary subsystem is defined by the feedback of the variables not on the path from the input to the response variable. If the sign of this subsystem’s feedback is positive then it will switch the sign of the path to the response variable, otherwise the sign of the path will be unchanged. The signed digraphs below illustrate the formation of feedback cycles that are used to predict perturbation response. All links that enter the input variable and all links leaving the response variable have been removed; products of the remaining links then become the feedback cycles, which determine the sign of the response. For response of _, feedback cycles will be composed of the following links (Figure 6):

Figure 6 A signed digraph of a predator–prey community of size n = 3, showing a perturbation scenario where there is a positive input to N2

Here two feedback cycles determine the sign of the response of due to an input to . One feedback cycle, , is formed by a path which goes directly from to , and it has a complementary subsystem in the negative self-effect of . The other cycle, , is composed of a path with negative sign of length two. This path lacks a complementary subsystem, in which case the sign of the path remains negative. Since both feedback cycles are negative, the equilibrium abundance of is predicted to decrease as a result of supplementation of .

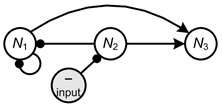
Next, consider the response of when there has been a negative input to , say through an increased rate of death, and note that for negative inputs the signs of the feedback cycles are switched. The sign of the response of is determined by the following links (Figure 7),

Figure 7 A signed digraph of a predator–prey community of size n = 3, showing a perturbation scenario where there is a negative input to N2

which form feedback cycles and . Here the response is ambiguous, as it is determined by feedback cycles of opposing sign.

3.1.1.4 Ambiguity and weighted predictions

The ambiguity in the response of can be resolved through consideration of symbolic inequalities. For instance, if it is believed that , then the predicted response of will be negative. Dealing with ambiguity in this manner requires a knowledge of relative strength of interaction and an ability to make sense of contingencies presented by symbolic arguments. However, in larger systems, complex inequalities can arise, which are too difficult to interpret or comprehend. In these instances the Assessment team can employ a heuristic technique of weighting the net number of feedback cycles to the absolute number in a response (i.e. the weighted prediction for a response prediction is equal to the net number of feedback cycles divided by the total number of cycles (Dambacher et al., 2002)).

For instance, the predicted response of for an input to is completely ambiguous, as there is the same number of positive and negative feedback cycles. But if there were, say, a total of four feedback cycles in a perturbation response, three of which were positive and one negative, then the net number of cycles would be two and the weighted prediction of the response would be 2/4 = 0.5. The sign determinacy of responses with weighted predictions ≥0.5 has been shown to generally be greater than 90% through simulations using random parameter space (Dambacher et al., 2003a; Hosack et al., 2008); below this threshold the sign determinacy of responses declines to zero for weighted predictions equal to zero.

3.1.2 Matrix algebra methods for qualitative mathematical modelling

The preceding section presents an overview of qualitative modelling based on a general interpretation of signed digraphs, this section presents an equivalent analysis based on a system’s community matrix, as derived from a system of equations. Computer programs for these analyses can be found in the most recent revision of Supplement 1 of Dambacher et al. (2002).

Rates of growth for n interacting populations can be described by a system of linear equations:

where the per capita rate of change in population abundance of is controlled by density-independent rates of birth , death , immigration and emigration, and density-dependent interactions. Generally stated as:

the growth function of each population is determined by the system’s variables () and growth rate parameters ; the latter can be collectively referred to as a vector p of length m. At equilibrium, population abundances (Ni^*) are unchanging and defined by:

In the neighborhood of an equilibrium point, density-dependent interactions, formally organised in the community matrix A (Levins, 1968), determine the balance between the column vectors of (the equilibrium population abundance), and k (the density-independent rates of growth), via , where . Elements of the community matrix are calculated as:

and essentially define the relationships or direct effects between system variables. Alternately, consider the system’s Jacobian matrix (A′), which is derived from the form of Equation (2) (i.e. ). The sign structure of the community and Jacobian matrices are identical, and thus for the purpose of qualitative modelling, either one can be used. Formal quantitative stability analyses, however, require use of the Jacobian matrix, although calculations of perturbation response can proceed with either the community or Jacobian matrix.

As previously discussed, the relationships between variables can be portrayed by signed digraphs, and for our example system with omnivory (Figure 5), the corresponding community matrix:

is equivalent in information content to the signed digraph.

A qualitative analysis of local or Lyapunov stability is based on the sign of the eigenvalues () of A, which are the roots of the characteristic equation formed by the equality:

where I is the identity matrix and ‘det’ is the matrix determinant. The resulting characteristic polynomial is of the form:

where , are the system’s polynomial coefficients. A system can be stable if and only if all eigenvalues of A have negative real parts:

For systems with five or more variables, an explicit solution of the roots is not possible, however, conditions for Equation (8) can be ensured through a series of n Hurwitz determinants constructed from the system’s polynomial coefficients:

Additionally, a necessary, but not sufficient condition for Equation (8) is that the polynomial coefficients have the same sign. The value of is arbitrarily +1 or –1, and for the convention of equating negative feedback with self damping it can be set equal to –1. This permits an alternative restatement of the conditions for stability via the criteria that: (i) polynomial coefficients are all negative, where ; and, (ii) Hurwitz determinants all are positive, where .

By these two criteria it is possible to understand stability in terms of the sign and balance of a system feedback (Puccia and Levins, 1985; Dambacher et al., 2003b). The polynomial coefficients describe the feedbacks F at each of n levels in a dynamical system, such that , , . The first criterion requires that feedback at each level be negative such that the system’s dynamics are self damped. Feedback cycles at the first level of a system are composed of the variable’s self-effects. For the example system, there are three feedback cycles at the first level: . In higher levels of the system, feedback cycles are products of either conjunct or disjunct links. At the second level there are six feedback cycles of length two that are products of either pairwise predator–prey links or the disjunct self-effects. All of these cycles have a negative sign: . Feedback at the highest level of the system is: . Here, there is one positive feedback cycle that involves the benefit that the top predator receives from omnivory. Stability in this system thus depends on the condition that the strength of this positive feedback cycle be less than the sum of the five negatively signed cycles.

The second stability criterion can be generally understood as a balance between higher and lower levels of feedback. A system that is dominated by higher level feedbacks can exhibit over correction and thus be prone to undamped oscillations. For a three-variable system the second criterion is:

which for our example system requires 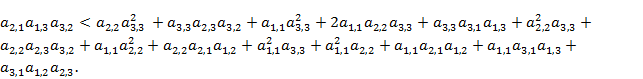Here stability depends on the feedback cycle with the negative effect that the basal species receives from omnivory be less than the sum of all other feedback cycles of length three and the products of lower level feedbacks. Stability in this system thus depends on the relative weakness of the omnivory interaction. Moreover, it can be inferred that if omnivory did not occur, then there would be no conditions for instability, in which case the system would be sign stable.

Any long-term impact on an ecosystem can be interpreted and evaluated as a sustained change in one of the system’s growth parameters. This is the case whether the change comes from within the system via a density-dependent parameter, as in Mendelian selection, or externally by way of a density-independent parameter, as in change coming from the environment or change from management, development or experimental purpose. The Assessment team is interested, then, in predicting change in the equilibrium level of each variable, and, through the implicit function theorem, the solution is by differentiation of Equation (2) with respect to :

Given the matrix equality:

where ‘det’ is the matrix determinant and ‘adj’ is the adjoint matrix, also known as a classical adjoint matrix, Equation (11) can be expressed more conveniently as:

Here is, via Cramer’s Rule (Lay, 2003), the solution for (the difference between the old and new equilibrium abundance for each population), and (the strength or magnitude of a given input or perturbation). For the example system, the solution for the effects of parameter change will be:

From Equation (14) it is evident the matrix A has two separate functions in determining a population’s response to a perturbation. Through the adjoint of A, all direct and indirect effects in the system are combined in complementary feedback cycles (Dambacher et al., 2002), which mediate the relative variation in the response of each population. The determinant of A constitutes the overall feedback of the system and scales the magnitude of each variable’s response to a perturbation. For example, for a given input, if the overall feedback is relatively weak, then the effect of the complementary feedback cycles on population abundance will be relatively large. For this system to be stable requires that det(–A) be positive, and from the above stability analysis, this requires that be relatively weak. Note that use of the determinant of –A maintains a sign convention in the adjoint matrix for even- and odd-sized systems (Dambacher et al., 2002). However, as previously mentioned, system feedback is normally considered to be negative in stable systems; this convention is reversed in Equation (13) and Equation (14) to analyse perturbation response.

In interpreting the adjoint matrix, a positive input to a variable – through an increase in birth rate or decrease in death rate – is read down a column, and response predictions for each variable are read along the rows. Here the correspondence between the matrix adjoint matrix in Equation (14) with the signed digraph analysis in the main text is seen. For a positive input to the prediction of decreased abundance of is determined by two feedback cycles of like sign (i.e. adjoint ), while the ambiguous response of is determined by two feedback cycles of opposing sign (i.e. adjoint). Where inputs to a variable are negative – through a decrease in birth rate or increase in death rate – then the signs of the adjoint matrix elements are simply reversed. In analysis of linear systems, multiple inputs will have an additive effect on the equilibrium of a variable through the superposition principle. Thus if there were simultaneous inputs that increased the birth rate of (e.g. by supplementation) and increased the death rate of (e.g. by culling), then the predicted response of would be calculated as: